La proposición es la expresión lingüística del razonamiento, que se caracteriza por ser verdadera o falsa empíricamente, sin ambigüedades. Son proposiciones las oraciones aseverativas, las leyes científicas, las fórmulas matemáticas, las fórmulas y/o esquemas lógicos, los enunciados cerrados o claramente definidos. No son proposiciones las opiniones y suposiciones; los proverbios, modismos y refranes; los enunciados abiertos no definidos; las oraciones interrogativas, exclamativas, imperativas, desiderativas y dubitativas; las interjecciones en general; ni las operaciones aritméticas.
El valor de verdad de una proposición depende no solamente de las relaciones entre las palabras del lenguaje y los objetos en el mundo, sino también del estado del mundo y del conocimiento acerca de ese estado. El valor de verdad de la oración Juan canta depende no solamente de la persona denotada en Juan y el significado del verbo cantar, sino también del momento cuando esta oración es expresada. Juan probablemente canta ahora, pero ciertamente que no siempre está cantando.
De la misma manera, debemos hacer una distinción entre la oración gramatical propiamente dicha, a la que llamaremos enunciado, y el contenido o significado del enunciado, que es la proposición. Así los siguientes enunciados representan en realidad a la misma proposición:
- En Maracaibo hace mucho calor
- Maracaibo es una ciudad muy calurosa
- La temperatura media de Maracaibo es bastante alta
- El clima de Maracaibo es cálido
- Maracaibo is a hot city
Las siguientes expresiones son ejemplos de proposiciones:
- Bolívar libertó a Venezuela
- El hierro es un mineral
- Einstein fue un físico teórico
- 36 + 63 = 99
- La palabra "esdrújula" es esdrújula
Los siguientes son ejemplos de expresiones las cuales no son proposiciones
- El hombre más fuerte del mundo
- El director del periódico
- ¡Quién se ganara el Kino!
- 13 + 7
- ¡Tú te callas!
- X obtuvo el Premio Nobel en 1970
- ¿Cuánto cuesta ese reloj?
Las proposiciones se representan por letras minúsculas: p, q, r, s, t, u, etc. Por ejemplo, sea la proposición q igual a 34 + 56 = 90
CLASIFICACION
Proposiciones Simples o Atómicas
Son aquellas que carecen totalmente de conectivos lógicos y que, por lo tanto, son inseparables. En este grupo se encuentran las proposiciones predicativas, que son aquellas en la cual se afirma o atribuye una característica respecto de un objeto, como por ejemplo, Juan Pérez es profesor; y las proposiciones relacionales, en las cuales existe una relación de dependencia, estableciendo un enlace entre dos o más objetos, como por ejemplo, Caracas es la capital de Venezuela.
Proposición Compuesta o Molecular
Son aquellas que resultan de la combinación de varias proposiciones simples, unidas por uno o más conectivos lógicos y que pueden ser separadas y descompuestas en proposiciones más simples. Su valor de verdad depende del de las proposiciones que la componen.
CONECTIVOS LÓGICOS
NEGACION

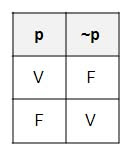
Tabla de Verdad de la Negación
CONJUNCIÓN

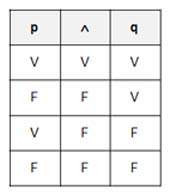

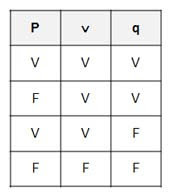





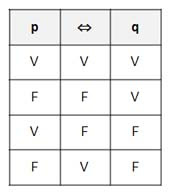
Tabla de Verdad de la Equivalencia






9 comentarios:
felicitaciones a la extension y calidad de las definiciones de los conceptos. Mas importante fueron los ejemplos y sus aplicaciones. Es necesario que las personas que entre al campo de la logica proposicional comprendan lo util y aplicable de este tema en la vida cotidiana hasta llegar al campo tecnologico y mas alla.
Gracias, reyii por sus comentarios.
Estamos trabajando en unas entradas sobre la aplicación de la teoría de conjuntos en los lenguajes Pascal (que tiene implementado el tipo de datos SET), y en C++ donde recurrimos de nuevo a los operadores lógicos binarios.
Consideramos que para dominar la programación de computadoras se deben dominar los conceptos de la lógica.
Gracias, muy buena informacion con explicaciones claras, ejemplos d aplcaciones y me ayudo bastante. salu2
jj chucho me alegra mucho que te haya servido el blog. Estamos preparando nuevas entradas sobre archivos y fechas, y otras más.
Siempre a la orden
Olas puxa super su pag ehh ants n t
ntendia nda peo aowa ya px + facil no podria star..graxias!!
Muy buenos los aportes realemente me sirvieron mil gracias
REALMENTE MUY BUENOS TUS APORTES EN CUANTO AL PROPOSICION LOGICA, SOLO FALTA TRADUCIRLO, PERO LA EXPLICACION ESTA MUY BUENA..THANK YOU SO MUCH..AND HAVE GREAT DAY.
Muchas gracias!!! muy buen contenido me ayudo bastante, tiene una informacion completa
Publicar un comentario