Implementación de Conjuntos en C/C++

Presentamos ahora la implementación de conjuntos en el lenguaje C/C++, el cual no cuenta con un tipo de datos específico, tal como el SET de Pascal, por lo que hemos recurrido a los operadores lógicos binarios, ya descritos en anteriores entradas (1)(2). 

Cada elemento de un conjunto de éstos está representado por un bit, y solamente permite datos de tipo base enteros, concretamente unsigned char. Se agrupan hasta 128 datos almacenados en un arreglo de 16 elementos. Veamos el código:

//Conjuntos.Cpp

#include "stdio.h"
#include "conio.h"
#include "alloc.h"

/* Definiciones */

#define M 128   // Elementos del conjunto
#define N 16     // Elementos del arreglo. M /8

unsigned char A[N], B[N], *C;
unsigned char x, y;

/* Prototipos de funciones */
void Iniciar (unsigned char C[]);
unsigned char byte (unsigned char x);
unsigned char bit (unsigned char x);
unsigned char Pertenece (unsigned char x, unsigned char C[]);
void Incluir (unsigned char x, unsigned char C[]);
void Excluir (unsigned char x, unsigned char C[]);
unsigned char *Union(unsigned char A[], unsigned char B[]);
unsigned char *Interseccion (unsigned char A[], unsigned char B[]);
unsigned char *Diferencia(unsigned char A[], unsigned char B[]);
unsigned char *Complemento (unsigned char A[]);
unsigned char Iguales(unsigned char A[], unsigned char B[]);
void Escribir (unsigned char C[]);
void Listar (unsigned char C[]);

void main() {
    // Iniciamos los conjuntos A y B
    Iniciar(A); Iniciar(B);
  
    // Agregamos algunos elementos al conjunto A
    for (x = 1; x < M; x *= 2)           // Potencias de 2
       Incluir(x, A);
    printf("A = "); Escribir(A);
  
    // Agregamos al conjunto B los multiplos de 20
    for (x = 20; x < M; x += 20)
        Incluir(x, B);
    printf("B = "); Escribir(B);

    // Hallamos la union de A y B en C
    C = Union(A, B);
    printf("Union de A y B = "); Escribir(C);

    // Hallamos la interseccion de A y B en C
    C = Interseccion(A, B);
    printf("Interseccion de A y B = "); Escribir(C);

    // Hallamos la diferencia de A y B en C
    C = Diferencia(A, B);
    printf("Diferencia de A y B = "); Escribir(C);

    // Hallamos complemento del conjunto A
    C = Complemento(A);
    printf("Complemento de A = "); Escribir(C);

    // Determinamos si los conjuntos A y B son iguales o diferentes
    if (Iguales(A, B))
        printf("\nA y B son iguales. \n");
    else
        printf("\nA y B son diferentes. \n");
    printf("\nA = "); Escribir(A);
    printf("\nB = "); Escribir(B);

    // Determinamos si los conjuntos A y C son iguales o diferentes
    C = A;
    if (Iguales(A, C))
        printf("\nA y C son iguales. \n");
    else
        printf("\nA y C son diferentes. \n");
    printf("\nA = "); Escribir(A);
    printf("\nC = "); Escribir(C);

    // Eliminamos algunos elementos del conjunto A
    Excluir(8, A); Excluir(32, A);
    printf("Despues de eliminar 8 y 32 de A.\n");
    printf("\nA = "); Escribir(A);
    getch();
}

/* ************************************************ */

/* Iniciar el conjunto */
void Iniciar (unsigned char C[])  {
    unsigned char i;
    for (i = 0; i < N; i++)
        C[i] = 0;
}

/* Determinar byte que ocupa el elemento x */
unsigned char byte (unsigned char x)  {
    return (x / 8);
}

/* Determinar el bit del byte que ocupa el elemento */
unsigned char bit (unsigned char x) {
    return (x % 8);
}

/* Incluir un elemento al conjunto */
void Incluir (unsigned char x, unsigned char C[]) {
    C[byte(x)] |= (1 << bit(x));
}

/* Excluir un elemento del conjunto */
void Excluir (unsigned char x, unsigned char C[]) {
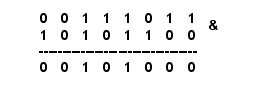
    C[byte(x)] &= (255 - (1 << bit(x)));
}

/* Determinar si un elemento pertenece al conjunto */
unsigned char Pertenece (unsigned char x, unsigned char C[]) {
    if (C[byte(x)] & (1 << bit(x)))  return 1;
    else return 0;
}

/* Unión de dos conjuntos */
unsigned char *Union(unsigned char A[], unsigned char B[]) {
unsigned char i, *C, *D;
    C = (unsigned char *)malloc(N);
    D = C;
    for (i = 0; i < N; i++)  {
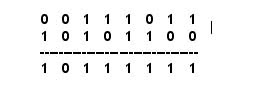
        *C = A[i] | B[i];
        C++;
    }
    return D;
}

/* Intersección de dos conjuntos */
unsigned char *Interseccion (unsigned char A[], unsigned char B[]) {
unsigned char i, *C, *D;
    C = (unsigned char *) malloc(N);
    D = C;
    for (i = 0; i < N; i++)  {
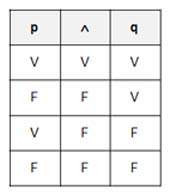
        *C = A[i] & B[i];
        C++;
    }
    return D;
}

/* Diferencia entre dos conjuntos */
unsigned char *Diferencia(unsigned char A[], unsigned char B[]) {
unsigned char i, *C, *D;
    C = (unsigned char *)malloc(N);
    D = C;
    for (i = 0; i < N; i++ )  {
        *C = A[i] & ~B[i];
        C++;
    }
    return D;
}

/* Hallar el complemento de un conjunto */
unsigned char *Complemento (unsigned char A[]) {
unsigned char i, *C, *D;
    C = (unsigned char *) malloc(N);
    D = C;
    for (i = 0; i < N; i++)  {
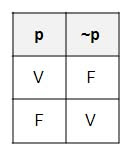
        *C = ~A[i];
        C++;
    }
    return D;
}

/* Determinar si dos conjuntos son iguales */
unsigned char Iguales(unsigned char A[], unsigned char B[]) {
unsigned char i;
    for (i = 0; i < N; i++)
        if (A[i] != B[i])  return 0;
    return 1;
}

// Determinar si un conjunto esta vacio
unsigned char Vacio(unsigned char C[]) {
unsigned char x;
    for (x = 0; x < N; x++)
        if (C[x] != 0)  return 0;
    return 1;
}

/* Escribir conjunto */
void Escribir (unsigned char C[]) {
unsigned char x;
    if  (!Vacio(C))  {
        printf("{ ");
        for (x = 0; x < M; x++)
            if (Pertenece(x, C))  printf("%u, ", x);
        printf("\b\b }"); // Borra la coma y el espacio anteriores
    }
    else  printf("{ }");
    printf("\n\n");
}

Implementación de Conjuntos en Pascal

El lenguaje Pascal cuenta con el tipo de datos SET que permite manejar información aplicando los conceptos básicos de la Teoría de Conjuntos. La definición de una estructura de este tipo tiene la forma siguiente:

TYPE nombre = SET OF tipo_base;

Donde tipo_base puede ser cualquier tipo ordinal, incluyendo los enumerados y los subrangos, pero con la limitación de un máximo de 255 elementos. Algunos ejemplos de conjuntos serían los siguientes:

TYPE  
     Dias = (Lunes, Martes, Miercoles, Jueves, Viernes, Sabado, Domingo);
     Puntos = 1..20;

     Conjunto1 = SET OF Dias;
     Conjunto2 = SET OF Puntos;
     Conjunto3 = SET OF BYTE;  

VAR
     A : Conjunto1;
     B : Conjunto2;
     C : Conjunto3;

Para representar un conjunto por extensión en Pascal se utilizan los símbolos [ y ], por ejemplo:

A := [Lunes, Jueves, Sabado];
B := [5, 9, 12, 16, 18];
C := [0..9, 15, 25, 44, 80..99];

Como podrán ver, pueden usarse subrangos en la enumeración de los elementos de un conjunto, tal como se permite en las matemáticas. Para representar el conjunto vacío se escriben los corchetes sin elementos, como en el siguiente ejemplo:

A := [ ];

Las funciones básicas de conjunto se ejecutan mediantes los siguientes operadores:

Unión :              +
Intersección :   *
Diferencia :       -
Subconjunto :   <=        
Pertenencia :   IN

Como muestra, presentamos un programa en Pascal donde se aplican algunas de estas funciones.

PROGRAM Conjuntos;
     USES CRT;
     
     TYPE Conjunto = SET OF Byte;
     
     VAR   A, B, C, D : Conjunto;
                N : ARRAY[1..100] OF BYTE;
                k, y : INTEGER;

(* Escribe los elementos de un conjunto *)
PROCEDURE EscribirConjunto(S : Conjunto);
     VAR  k : BYTE;
Begin
    IF NOT (S = []) THEN
    begin
        Write('{ ');
        For k := 0 TO 255 DO
            IF k IN S THEN Write(k, ', ');
        Writeln(CHR(8), CHR(8),  ' }');
    end
    ELSE
    Writeln('{ }');
    Writeln; Writeln;
End;

(* Incluye elementos en el conjunto A *)
PROCEDURE IncluirElementos;
     VAR x, y : BYTE;
Begin
    REPEAT
         ClrScr;
         gotoXY(10, 10); Write('Escriba un número (0 - 255) : ');
         Readln(x);
         A := A + [x];
         gotoXY(10, 12); Write('Desea continuar (1 = Si, 2 = No) ? ');
         Readln(y);
    UNTIL (y = 2);
End;

(* Incluir en el conjunto B los números potencia de 2 *)
PROCEDURE CrearConjunto;
     VAR k : INTEGER;
Begin
    k := 2;
    WHILE (k <= 255) DO
    begin
        B := B + [k];
        k := k * 2;
    end;
End;

(* Rellenar un arreglo de números aleatorios sin repeticiones *)
PROCEDURE RellenarArreglo;
     VAR i, j, k, x, t : BYTE;
              S : Conjunto;
Begin
    S := []; (* Inicialmente el conjunto está vacío *)
    Randomize;
    FOR k := 1 TO 100 DO
    begin
        REPEAT
             x := Random(256);       (* El tipo BYTE acepta 256 valores. *)
        UNTIL NOT (x IN S);      (* Evita que hayan elementos repetidos. *)
        N[k] := x;
        S := S + [x];                        (* Incorporamos x al conjunto *)
    end;

(* Ordenamos el arreglo ascendentemente *)
FOR i := 1 TO 99 DO
     FOR j :=  i + 1 TO 100 DO
          IF N[i] > N[j] THEN
          begin
              t := N[i];
              N[i] := N[j];
              N[j] := t;
          end;
End;

PROCEDURE EscribirAyB;
Begin
    ClrScr;
    Write('A = '); EscribirConjunto(A);
    Write('B = '); EscribirConjunto(B);
    ReadKey;
End;

PROCEDURE OperacionesBasicas;
Begin
    ClrScr;
    A := [2, 4, 6, 8, 10, 12, 14, 16, 18, 20];
    B := [3, 6, 9, 12, 15, 18, 21, 24, 27, 30];
    gotoXY(4, 10); Write('A = '); EscribirConjunto(A);
    gotoXY(4, 12); Write('B = '); EscribirConjunto(B);

    (* Unión de los conjuntos A y B *)
    C := A + B;
    gotoXY(4, 14); Write('A U B = '); EscribirConjunto(C);
    
    (* Intersección de los conjuntos A y B *)
    C := A * B;
    gotoXY(4, 16); Write('A ', CHR(239), ' B = '); EscribirConjunto(C);

    (* Diferencia entre los conjuntos A y B *)
    C := A - B;
    gotoXY(4, 18); Write('A - B = '); EscribirConjunto(C);
    ReadKey;
End;

PROCEDURE OtrasOperaciones;
Begin
    ClrScr;
    (* A es el conjunto de los pares *)
    A := [];
    k := 2;
    WHILE (k <= 255) DO
    begin
        A := A + [k];
        k := k + 2;
    end;
    
    (* C es el complemento de A *)
    C := [];
    FOR k := 0 TO 255 DO
         IF NOT (k IN A) THEN
            C := C + [k];
    
    (* D es el conjunto de los múltiplos de 4 *)
    D := [];
    k := 4;
    WHILE (k <= 255) DO
    begin
        D := D + [k];
        k := k + 4;
    end;
    Write('A = '); EscribirConjunto(A);
    Write('B = '); EscribirConjunto(B);
    Write('C = '); EscribirConjunto(C);
    Write('D = '); EscribirConjunto(D);

    (* D es subconjunto de A *)
    IF D <= A THEN         Writeln('D es subconjunto de A')
    ELSE
       Writeln('D no es subconjunto de A');
    ReadKey;
End;

PROCEDURE Arreglos;
Begin
    ClrScr;
    (* Un arreglo de 100 elemetos sin repeticiones *)
    RellenarArreglo;
    Writeln('Arreglo N: ');
    For k := 1 TO 100 DO
        Write(N[k]:4);
    ReadKey;
End;

PROCEDURE VaciarConjuntos;
Begin
    A := [];
    B := [];
    C := [];
    D := [];
End;

BEGIN
     REPEAT
          ClrScr;
           gotoXY(10, 4); Write('1. Incluir Elementos en A');
           gotoXY(10, 6); Write('2. Crear Conjunto B');
           gotoXY(10, 8); Write('3. Escribir A y B');
           gotoXY(10, 10); Write('4. Operaciones Básicas');
           gotoXY(10, 12); Write('5. Otras Operaciones');
           gotoXY(10, 14); Write('6. Arreglos');
           gotoXY(10, 16); Write('7. Vaciar Conjuntos');
           gotoXY(10, 18); Write('0. Salir');
           gotoXY(10, 20); Write('Su Selección --> ');
          Readln(y);
          CASE y OF
               1 : IncluirElementos;
               2 : CrearConjunto;
               3 : EscribirAyB;
               4 : OperacionesBasicas;
               5 : OtrasOperaciones;
               6 : Arreglos;
               7 : VaciarConjuntos;
               0 : Exit;
          End;
     UNTIL y = 0;
END.

TEORÍA DE CONJUNTOS - Conceptos Básicos

Operadores Lógicos Binarios – Segunda Parte

Presentamos ahora algunas aplicaciones utilizando los operadores lógicos binarios, implementando una biblioteca de funciones de utilidad general, y un pequeño programa demostrativo de dichas funciones, las cuales pasamos a describir brevemente, aclarando que los números manejados son del tipo unsigned char, es decir, números enteros positivos de un byte.

printbits: Recibe un número en decimal y lo escribe en binario. Utiliza la función condicional implícita.

onoff: Recibe un número en decimal y la posición de un bit, y determina si ese bit está encendido (1) o apagado (0).

put_on: Recibe un número en decimal y la posición de un bit y lo enciende, es decir, lo convierte en 1.

put_off: Recibe un número en decimal y la posición de un bit y lo apaga, es decir, lo convierte en 0.

right_rot : Recibe un número en decimal (x) y un número entre 0 y 7 (n), y rota n posiciones a la derecha los bits de x.

left_rot : Recibe un número en decimal (x) y un número entre 0 y 7 (n), y rota n posiciones a la izquierda los bits de x.

change_nibbles: Recibe un número en decimal e Intercambia sus nibbles.

right_nibble: Recibe un número en decimal y devuelve su nibble derecho

left_nibble: Recibe un número en decimal y devuelve su nibble izquierdo


// Biblioteca de funciones de manipulacion de bits
// bits.h

#include <stdio.h>

// Escribe un numero en binario
void printbits(unsigned char x) {
for (int i = 7; i >= 0; i--)
   printf("%c", (x & (1 << i)) ? '1' : '0');
}

// Determina si el bit n de un byte esta encendido (1) o apagado (0)
unsigned char onoff(unsigned char x, unsigned char n) {
     if (x & (1 << n)) return 1;
     else return 0;
}

// Enciende un bit
unsigned char put_on(unsigned char x, unsigned char n) {
     return x |(1 << n);
}

// Apaga un bit
unsigned char put_off(unsigned char x, unsigned char n) {
     return x & (255 - (1 << n));
}

// Realiza la rotacion a la derecha
unsigned char right_rot(unsigned char x, unsigned char n) {
     return (x >> n) | (x << (8 - n));
}

// Realiza la rotacion a la izquierda
unsigned char left_rot(unsigned char x, unsigned char n) {
    return (x << n) | (x >> (8 - n));
}

// Intercambia los nibbles (4 bits) de un byte
unsigned char change_nibbles(unsigned char x) {
     return (x << 4) | (x >> 4);
}

// Obtiene el nibble izquierdo
unsigned char left_nibble(unsigned char x) {
     return x >> 4;
}

// Obtiene el nibble derecho
unsigned char right_nibble(unsigned char x) {
     return x & 15;
}

Listado 1. bits.h


Y ahora el programa ejemplo para demostrar el uso de las funciones de la biblioteca.

// Manejo de bits
// bits.cpp

#include <stdio.h>
#include <conio.h>
#include <C:\BC5\Programas\bits.h>  // Ubicar la ruta del archive de biblioteca

unsigned char m1, m2, n1, n2, x, y, z;

void NuevaLinea();

void main() {
    m1 = m2 = 59;
    n1 = n2 = 172;

    printf("Valores originales.\n");
    printf(" 76543210\n");
    printf("m1 = %3d = ", m1); printbits(m1); NuevaLinea();
    printf("n1 = %3d = ", n1); printbits(n1); NuevaLinea();

    printf("El bit 4 de m1 vale %d\n", onoff(m1, 5) ? 1 : 0);
    printf("El bit 4 de n1 vale %d\n", onoff(n1, 4) ? 1 : 0);
    NuevaLinea();

    printf("Se enciende el bit 6 de %3d. Resultado en x.\n", m2);
    x = put_on(m2, 6);
    printf(" 76543210\n");
    printf(" x = %3d = ", x); printbits(x); NuevaLinea();
    printf("El bit 6 de x vale %d\n", onoff(x, 4) ? 1 : 0);
    NuevaLinea();

    printf("Se apaga el bit 5 de %3d. Resultado en y.\n", n2);
    y = put_off(n2, 5);
    printf(" 76543210\n");
    printf(" y = %3d = ", y); printbits(y); NuevaLinea();
    printf("El bit 5 de y vale %d\n", onoff(y, 5));
    NuevaLinea();

    m2 = m1; n2 = n1;
    printf("%3d se rota 3 bits a la derecha. Resultado en x.\n", m2);
    x = right_rot(m2, 3);
    printf(" 76543210\n");
    printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
    printf(" x = %3d = ", x); printbits(x); NuevaLinea();
    NuevaLinea();

    printf("%3d se rota 3 bits a la izquierda. Resultado en y.\n", n2);
    y = left_rot(n2, 3);
    printf(" 76543210\n");
    printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
    printf(" y = %3d = ", y); printbits(y); NuevaLinea();
    NuevaLinea();

    m2 = m1; n2 = n1;
    printf("Se intercambian los nibbles de %3d. Resultado en x.\n", m2);
    x = change_nibbles(m2);
    printf(" 76543210\n");
    printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
    printf(" x = %3d = ", x); printbits(x); NuevaLinea();
    NuevaLinea();

    printf("Se intercambian los nibbles de %3d. Resultado en y.\n", n2);
    y = change_nibbles(n2);
    printf(" 76543210\n");
    printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
    printf(" y = %3d = ", y); printbits(y); NuevaLinea();
    NuevaLinea();

    m2 = m1; n2 = n1;
    printf("Se obtiene el nibble izquierdo de %3d. Resultado en x.\n", m2);
    x = left_nibble(m2);
    printf(" 76543210\n");
    printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
    printf(" x = %3d = ", x); printbits(x); NuevaLinea();
    NuevaLinea();

    printf("Se obtiene el nibble derecho de %3d. Resultado en y.\n", n2);
    y = right_nibble(n2);
    printf(" 76543210\n");
    printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
    printf(" y = %3d = ", y); printbits(y); NuevaLinea();
    NuevaLinea();

getch();

}

void NuevaLinea() {
    printf("\n");
}

Listado 2. bits.cpp

Operadores Lógicos Binarios – Primera Parte

En el siglo XIX el matemático inglés George Boole formuló todo un cuerpo de teoría donde hace una correspondencia entre los valores veritativos de la Lógica Formal, verdadero y falso, con los números 0 y 1 respectivamente, y la cual se conoce hoy como el Álgebra de Boole. En aquella época quizás muchos se preguntarían para qué podría servir semejante conjunto de definiciones, operaciones y leyes basadas sólo en 2 números. Un siglo después Claude Shannon encontró otra correspondencia, esta vez entre el Álgebra de Boole y los conmutadores electrónicos, introduciendo así el concepto de bit, abriendo de esta manera el camino a la aplicación práctica de esta teoría, que se plasmaría en los denominados circuitos lógicos, base de los sistemas de computación modernos. (1)

Casi todos los lenguajes de programación implementan tipos de datos lógicos o booleanos, y sus respectivos operadores, conocidos generalmente por sus nombres en inglés (and para la conjunción, or para la disyunción inclusiva, xor para la disyunción exclusiva y not para la negación. La implicación está implícita en la sentencia condicional if) (2). Pero también podemos realizar las operaciones lógicas a nivel de los bits de números enteros, a través de los operadores lógicos binarios (bitwise), además de otras como el desplazamiento y la rotación de bits, en lenguajes como C.

Primero veamos los operadores lógicos formales, o sea, aquellos cuyos operandos son expresiones lógicas como las obtenidas mediante los operadores relacionales; recordando además que en el lenguaje C y sus derivados el 0 representa el valor lógico falso y cualquier otro número, generalmente el 1, representa el valor lógico verdadero.

La conjunción se realiza mediante el operador &&, y como hemos visto, el resultado sólo es verdadero si ambos operadores son verdaderos. Ejemplo:

int m = 4, n = 5, p;
p = (m > 0) && (n == 5);
// ambas operaciones relacionales son verdaderas.
// p toma el valor de 1 (verdadero)

if ( (m > n) && (n > 1) ) p = 10;
else p = 20;
// p vale 20, ya que (m > n) es falso y, por tanto, la conjunción
// es falsa

La disyunción inclusiva se lleva a cabo con el operador ||, y es falsa solamente si los dos operandos son falsos. Ejemplo:

int a = 1, b = 2, c = 3;
if ( (a > b) || (c >= a + b) ) c++;
else c = 0;
// como (c >= a + b) es verdadera, la disyunción inclusiva
// es verdadera, y c se incrementa en 1 (c++)

La negación tiene como operador el signo ! e invierte el valor de su único operando lógico. Ejemplo:

int x = 3, y;
if (!x) y = 100;
else y = 10;
// como x es distinto de 0, o sea, verdadero, al negarlo con ! se
// convierte en falso. La variable y vale 10

En cuanto a los operadores lógicos binarios, en C/C++ tenemos los siguientes:

Conjunción Binaria: &.

Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m & n será:

Disyunción Inclusiva Binaria: |

Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m | n será:

Disyunción Exclusiva Binaria: ^:

Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m ^ n será:



Negación Binaria (Conocida también como complemento a 1): ~.

Sea m = 59 (00111011₂), entonces ~n será:


Si observamos el valor resultante, comprobamos que se trata del número 196 en decimal, el cual sumado al operando original, o sea el 59, nos da 255, lo que es lo mismo que 2⁸ - 1. En general, el complemento a 1 de un número m de n bits será: ~m = 2ⁿ - m - 1. Si se elimina el -1, hablaríamos del complemento a 2; por lo tanto, el complemento a 2 de un número m es: ~m + 1, que es utilizado para representar números enteros negativos en la computadora.

Las operaciones de desplazamiento de bits permiten justamente eso, mover los bits de un byte, bien sea a la derecha o a la izquierda. Son de mucha utilidad en diversas situaciones, incluso para realizar operaciones aritméticas. Veamos su implementación en el lenguaje C:

Desplazamiento a la Izquierda: <<.

Sea m = 59 (00111011₂), entonces n >> 2 será:

Obsérvese que los bits del número se desplazan 2 espacios a la izquierda, rellenando con 0 los bits menos significativos (los de la derecha). En este caso, si desplazamos más de 2 bits a la izquierda, se perderían bits, lo que se conoce como acarreo. En cuanto al valor resultante, vemos que se trata de 236, o sea, 59 * 4; en general, el desplazamiento a la izquierda de n bits de un número m es igual a: m << n = m * 2ⁿ, siempre y cuando no haya pérdida de bits (acarreo).

Desplazamiento a la Derecha: >>.
Sea n = 172 (10101100₂), entonces n >> 2 será:


Aquí los bits del número se desplazan 2 espacios a la derecha, rellenando con 0 los bits más significativos (los de la izquierda). Igualmente, si desplazamos más de 2 bits se perderían bits. El resultado es 43, es decir, 172 / 4; en general, el desplazamiento a la derecha de n bits de un número m es igual a: m >> n = m / 2ⁿ, siempre y cuando no haya pérdida de bits (acarreo).

Proposición Lógica

Definición. Una proposición es una oración con valor referencial o informativo, de la cual se puede predicar su veracidad o falsedad, es decir, que puede ser falsa o verdadera pero no ambas a la vez.

La proposición es la expresión lingüística del razonamiento, que se caracteriza por ser verdadera o falsa empíricamente, sin ambigüedades. Son proposiciones las oraciones aseverativas, las leyes científicas, las fórmulas matemáticas, las fórmulas y/o esquemas lógicos, los enunciados cerrados o claramente definidos. No son proposiciones las opiniones y suposiciones; los proverbios, modismos y refranes; los enunciados abiertos no definidos; las oraciones interrogativas, exclamativas, imperativas, desiderativas y dubitativas; las interjecciones en general; ni las operaciones aritméticas.

El valor de verdad de una proposición depende no solamente de las relaciones entre las palabras del lenguaje y los objetos en el mundo, sino también del estado del mundo y del conocimiento acerca de ese estado. El valor de verdad de la oración Juan canta depende no solamente de la persona denotada en Juan y el significado del verbo cantar, sino también del momento cuando esta oración es expresada. Juan probablemente canta ahora, pero ciertamente que no siempre está cantando.

De la misma manera, debemos hacer una distinción entre la oración gramatical propiamente dicha, a la que llamaremos enunciado, y el contenido o significado del enunciado, que es la proposición. Así los siguientes enunciados representan en realidad a la misma proposición:

• En Maracaibo hace mucho calor
  
• Maracaibo es una ciudad muy calurosa
  
• La temperatura media de Maracaibo es bastante alta
  
• El clima de Maracaibo es cálido
  
• Maracaibo is a hot city
  

Las siguientes expresiones son ejemplos de proposiciones:

• Bolívar libertó a Venezuela
  
• El hierro es un mineral
  
• Einstein fue un físico teórico
  
• 36 + 63 = 99
  
• La palabra "esdrújula" es esdrújula
  

Los siguientes son ejemplos de expresiones las cuales no son proposiciones

• El hombre más fuerte del mundo
  
• El director del periódico
  
• ¡Quién se ganara el Kino!
  
• 13 + 7
  
• ¡Tú te callas!
  
• X obtuvo el Premio Nobel en 1970
  
• ¿Cuánto cuesta ese reloj?
  

Las proposiciones se representan por letras minúsculas: p, q, r, s, t, u, etc. Por ejemplo, sea la proposición q igual a 34 + 56 = 90

CLASIFICACION

Proposiciones Simples o Atómicas

Son aquellas que carecen totalmente de conectivos lógicos y que, por lo tanto, son inseparables. En este grupo se encuentran las proposiciones predicativas, que son aquellas en la cual se afirma o atribuye una característica respecto de un objeto, como por ejemplo, Juan Pérez es profesor; y las proposiciones relacionales, en las cuales existe una relación de dependencia, estableciendo un enlace entre dos o más objetos, como por ejemplo, Caracas es la capital de Venezuela.

Proposición Compuesta o Molecular

Son aquellas que resultan de la combinación de varias proposiciones simples, unidas por uno o más conectivos lógicos y que pueden ser separadas y descompuestas en proposiciones más simples. Su valor de verdad depende del de las proposiciones que la componen.

CONECTIVOS LÓGICOS

NEGACION

Tabla de Verdad de la Negación

 
CONJUNCIÓN

 Tabla de Verdad de la Conjunción

DISYUNCION INCLUSIVA

 Tabla de Verdad de la Disyunción Inclusiva

DISYUNCION EXCLUSIVA

Tabla de Verdad de la Disyunción Exclusiva

IMPLICACIÓN

Tabla de Verdad de la Implicación

EQUIVALENCIA

Tabla de Verdad de la Equivalencia

 

Ordenador o Computadora

Los hispanohablantes del lado americano del Atlántico sentimos, en general, una gran molestia o simplemente extrañeza, al ver u oír la palabra ordenador para referirse a esa omnipresente máquina que todos por aquí llamamos computadora, o computador en algunos casos. El porqué de esta diferencia es el tema que trataremos de seguidas, basados principalmente en un artículo de profesor de la Universidad Complutense de Madrid Antonio Vaquero Sánchez¹, y un pequeño libro escrito por el francés Claude Bellavoine² a finales de los años 60's.

Pensamos que las diferencias para denominar diversos objetos de uso diario entre las numerosas regiones que tienen el idioma español o castellano como medio de comunicación oral y escrita no constituyen en sí mismo ninguna anomalía, y no se pueden considerar como peligrosas para la conservación y buen uso del mismo. Así tenemos que en algunos países se usa cacerola para referirse a los objetos que en otros sitios se denominan ollas, y lo mismo ocurre con carro y coche. Igualmente pasa con los nombres de animales y vegetales, como en el caso de gambas y camarones, aguacate y palta, piña y ananás, merey y marañón, etc.

En el caso de la terminología científica y tecnológica, sin embargo, este asunto debe ser tratado con mayor rigor, ya que cualquier documento que tenga la pretensión de ser difundido en los ambientes académicos, gubernamentales y de organizaciones internacionales debe ser manejado con un léxico normalizado bien preciso y coherente. Para esto deben tomarse en consideración el origen, la amplitud o universo de uso, y la precisión de cada término referido a algún concepto u objeto de carácter científico y tecnológico. Para corroborar la importancia de este planteamiento nos podemos remitir al conocido portal web Wikipedia.org en su versión en español, el cual a través de un wikiproyecto denominado Terminología Informática, en el cual intervinieron muchos de sus colaboradores de ambos lados del Atlántico, estableció una normativa para la nomenclatura de los términos técnicos a utilizarse en sus artículos con la temática informática³. (A propósito, nuestro próximo artículo se refiere al uso de las palabras Informática y Computación).

Comencemos entonces con fragmentos del artículo del profesor Vaquero Sánchez titulado "Uso de la palabra Ordenador":

"(…) En España el término ordenador está muy extendido para designar a la máquina por excelencia de la Informática. Hay una minoría, en general universitaria, que usa indistintamente los términos computadora (o computador) y ordenador. Mucho menos somos los que sólo usamos el término computadora. Pero solamente en España se usa la palabra ordenador, que es absolutamente desconocida en América. La comunidad americana de habla española sólo usa la palabra computador y también computadora, aunque esta última en menor medida.

"(…) Antes que ordenador, en España se usó la palabra calculadora. Calculator aparece antes que computer en la literatura germinal de las computadoras. Así, la máquina desarrollada en 1944, bajo la dirección del Profesor Aiken en la Universidad de Harvard, era referida como Mark I o Automatic Sequence Calculator. El profesor García Santesmases pasó un tiempo trabajando con el grupo de las Marks. Por él se introdujo en nuestro país la palabra calculadora, para designar lo que mucho después se llamaría ordenador. Calculadora fue pues el primer término con que se conocieron estas máquinas en España, término que se usó extensamente en la década de los 60, como se comprueba más adelante, e incluso llega a la de los 70. Desde entonces se aplica sólo a las máquinas de mano con teclas numéricas y funcionales.

"Vamos a rastrear ahora el origen de la palabra ordenador. Trasladémonos a Francia. Hacia 1962 aparecen dos palabras nuevas en los ambientes universitarios franceses: Informatique y Ordinateur. Ambas tienen una rápida difusión y aceptación en el país vecino. Por ejemplo en 1963 ya existía en la Facultad de Ciencias de la Universidad de Toulouse un Laboratoire d'Informatique. En España se adoptó rápidamente la palabra Informática, pero esa rapidez no se dio con la palabra ordenador. Prueba de ello es la traducción del libro Vocabulary of Infomation Processing, (…) computer se tradujo por calculadora.

"La palabra ordenador aparece escrita por primera vez en un diccionario de Informática en español en 1972. Es el Diccionario-Glosario de Proceso de Datos Inglés-Español, IBM, 1972. La adopción del galicismo tiene un éxito fulgurante, directamente proporcional al crecimiento de usuarios de Informática, influidos por los profesionales comerciales. El origen ya lo conocemos. Ahora bien, vamos al fondo. ¿Qué significa ordinateur? No se debe entrar al trapo de los que defienden el uso de la palabra ordenador porque éste realiza ordenaciones (operaciones de ordenación). Puede hacer más, muchísimo más, que ordenar elementos ordenables. Admitir esa denominación por esa causa sería como admitir la designación del todo por una parte solamente.

"Tampoco es válido el argumento basado en la acepción de orden como instrucción. Ordinateur viene definido en francés así "... qui émite ordres". En definitiva, quien da órdenes, no quien las recibe. Por tanto, el uso de la palabra ordenador es una incorrección semántica. (…) Lo dicen los propios franceses. Los mismos que contribuyeron a la creación, difusión y aceptación del término.

"¿Qué hacemos aquí sobre la utilización de los diversos términos? (…) Los hispanoparlantes de otros continentes (…) siempre usan computador/a. Y no van a cambiar. Tienen la razón de la fuerza numérica, pues son casi 10 veces más que nosotros. Y nosotros, los españoles, carecemos de argumentos lingüísticos sólidos para convencerles. ¿Qué podemos hacer aquí? Sería más lógico que, si hay que hacer algún cambio, lo hiciésemos nosotros. Deberíamos hacerlo en aras de la cohesión de nuestra lengua. (…) En cuanto al género, éste carece de importancia. Un computador (masculino) es un sistema (masculino) y una computadora (femenino) es una máquina (femenino). Pero es curioso que sólo se diga ordenador y no ordenadora. Esta curiosidad queda para los estudiosos de los fenómenos sociolingüísticos."

Ahora bien, ¿por qué los franceses utilizan el término ordenador (ordinateur)? La respuesta la hallamos en el libro de Bellavoine y es a mi parecer francamente absurda. Veamos entonces el origen de la palabra ordenador (Las negritas y cursivas son nuestras):

"En 1954, la Compañía IBM de Francia tropezó con el problema de traducir la denominación "Electronic Data Processing Machine" (EDPM). (…) No quería usar el término "Computadora", aunque los primeros trabajos eran sobre todo de índole científica, porque esa palabra hubiera limitado las posibilidades de utilización y, por consiguiente, de venta de esa máquina y no expresaba en forma adecuada la innovación técnica. La expresión "Machines électroniques a données processionnelles" ("Máquinas Electrónicas procesadoras de datos"), en la que se había pensado por un momento, sonaba extraña. En efecto, más tarde, la palabra inglesa "data" se tradujo por "datos" y luego por "información", mientras que "Processing" se convirtió en "procesamiento" y también en "tratamiento"; esto dio lugar a nuestra definición. Los estadounidenses, a su vez, inventaron un término más sencillo, el de computadora.

La IBM de Francia se dirigió entonces al profesor Jacques Perret, de la Facultad de Letras de París, y éste propuso que se volviera a introducir una palabra teológica, ¡caída en desuso desde hacía 600 años¡, la palabra "Ordenador". Dios era el gran Ordenador del Universo, es decir, el que ordena las cosas de acuerdo con un plan. Modestamente, el término se juzgaba digno de las nuevas máquinas cuyo porvenir se vislumbraba. La definición se aplicó, pues, a las nuevas EDPM, capaces de ordenar informaciones dispersas en función de un objetivo preciso."

Como diría un francés: "Mon Dieu!"

En un foro⁴ sobre el tema un ingeniero de sistemas español, cuyo nombre lamentablemente no aparece, dijo lo siguiente:

"(…) Efectivamente, el desafortunado término de "ordenador" (copiado sin criterio de los franceses) se usó por primera vez en España a principios de los 70, pero no fue sino hasta los 80 que se popularizó, con las PCs. Hasta ese momento todos decíamos "Computadora". (…) La carrera que yo estudié se llamaba oficialmente en casi todas la Universidades españolas "Ciencias de la Computación", y ese nombre aún estaba en uso hasta no hace tanto en varias universidades.

(…) Este es un término que nos viene del latín, y su raíz está en nuestro vocabulario desde hace siglos. Las Computadoras, es decir las máquinas de cómputo, no hacen muchas cosas; sólo hacen una cosa: computar ceros y unos. (…) En definitiva, la Academia de la Lengua en España, tradicionalmente compuesta por personas muy influidas por la cultura francesa y en aquellos años con escasísimos conocimientos técnicos, optaron acríticamente por separarse de lo que era una práctica extendida y natural en nuestro idioma, decir "Computadora". Aún conservo mis primeros libros editados e impresos en España donde sólo se usaba ese término."

Efectivamente, creo que la clave de todo este asunto es que hablamos de una máquina (o sistema) que es capaz de procesar muchísimos tipos de datos, como números, textos, gráficos, fotografías y videos, entre otros, pero a la larga todo su trabajo se reduce a computar ceros y unos, como dice nuestro anónimo amigo español. Así se trate de un video-juego, una aplicación ofimática, un navegador de Internet, lo que sea que se ejecute en una computadora será computable.

 

1. www.elmundo.es/su-ordenador/SORnumeros/97/SOR066/SOR066tribuna.html
   
2. Claude Bellavoine.- ¿Qué es una Computadora? Editorial El Ateneo. Buenos Aires. 1973. Traducción de la obra en francés Qu'est-ce qu'un ordinateur?. 1969.
   
3. (http://es.wikipedia.org/wiki/Wikiproyecto:Terminología_Informática)
   
4. http://86400.es/2007/04/17/¿-ordenador-o-computador-la-cohesion-del-lenguaje/
   

Charles Babbage – Padre de la Computación

Aunque pudiéramos considerar a la computadora el invento más característico de nuestro tiempo, sus antecedentes se remontan a más de 150 años cuando un matemático inglés diseñó y construyó una máquina que por su estructura y las funciones que debía desarrollar constituye, sin dudas, el primer prototipo de computadora jamás construido.

Charles Babbage, nacido el 26 de diciembre de 1791 en Devonshire, Inglaterra, fue uno de los dos niños sobrevivientes de Benjamín Babbage, banquero, y Beatriz Plumleigh Teapen. Siendo un niño débil y enfermizo, el pequeño Charles padeció de una severa fiebre, que hizo que sus padres temieran por su vida y, buscando su recuperación, decidieron enviarlo a Teignmouth por un tiempo, lo que ha ocasionado confusiones sobre su lugar de nacimiento en algunos de sus biógrafos.

En octubre de 1810 Babbage ingresó al Trinity College en Cambridge donde estudió matemáticas y química. Obtuvo su licenciatura en matemáticas en 1814, graduándose como el primero en su clase, y posteriormente ingresó a la maestría en matemáticas a Cambridge, de donde se graduó en 1817. En 1816 fue elegido miembro de la Royal Society donde jugó un papel preponderante en la fundación de la Sociedad Astronómica Real en 1820, y ya en 1828 ingresó en su universidad como profesor de Matemáticas.

Se dice que durante sus años universitarios, Babbage se mostró un tanto decepcionado al descubrir que las matemáticas de Newton, que había muerto 200 años antes, seguían vigentes en Cambridge, sin mayor evolución, e ignorando todos los avances que se habían dado en diversas partes del mundo. Babbage se convenció de que sus conocimientos de matemáticas eran superiores a los de sus maestros, y decidió fundar la Sociedad Analítica, junto con H.F.W. Herschel y George Peacock, con el propósito de renovar la enseñanza de las matemáticas en Inglaterra. Fue precisamente durante una de las reuniones de la Sociedad Analítica en la que se cuenta que Babbage estaba distraído contemplando una tabla de logaritmos que se encontraba frente a él y alguien se le acercó a preguntarle: "Bien, Babbage, ¿en qué sueñas?", a lo que él respondió, mientras señalaba la tabla: "Creo que todas estas tablas podrían ser calculadas por una máquina". Babbage había constatado que muchos de los cálculos consistían en operaciones que había que repetir de manera regular, y desde este punto de vista especuló que debería ser posible diseñar una máquina calculadora que pudiera hacer estas operaciones de forma automática.

La carrera de Babbage como inventor y como autor fue muy prolífica. Dentro de sus inventos más destacados se encuentra el dinamómetro, las tarifas postales uniformes, los atrapa-vacas motorizados, las luces ocultas de los faros, el oftalmoscopio heliográfico y el velocímetro. Además, calculó las primeras tablas de mortalidad confiables, utilizadas todavía por las compañías de seguros. Asimismo, se le considera uno de los pioneros de la investigación de operaciones. Publicó alrededor de 80 libros y artículos en áreas que van desde las matemáticas hasta la teología, astronomía y política.

La Máquina Diferencial

Babbage tenía un gran interés por las máquinas calculadoras, y estudió la posibilidad de construir una máquina capaz de calcular con exactitud. En 1822 construyó la primera de sus máquinas, que podía sumar números hasta de seis cifras. Animado por el éxito continuó sus estudios y, en 1823, diseñó una máquina más elaborada a la que llamó "Máquina Diferencial", que debía estar provista de una impresora. Pero para fabricar el primer modelo necesitaba dinero (1,500 libras esterlinas) que le fue proporcionado por el gobierno, comprometiéndose Babbage a entregar la máquina en dos años. Sin embargo, la construcción avanzaba muy lentamente y, al cumplirse el plazo en 1827, la máquina aún no estaba terminada.

La Máquina Diferencial era capaz de calcular los logaritmos de 1 a 108.000 con notable precisión e imprimirlos, y formuló los fundamentos teóricos de cualquier autómata de cálculo. Por entonces Babbage ya conocía los sistemas decimales de conteo, y estaba familiarizado con la descomposición de complejas operaciones matemáticas en secuencias sencillas. La presentó en la Real Sociedad Astronómica de Londres, recibiendo por ella la Medalla de Oro de dicha sociedad. Fue entonces cuando obtuvo una subvención para diseñar y construir una máquina en diferencias más grande. Babbage esperaba terminarla en 3 años pero la construcción se alargó
en el tiempo. En 1834 se paró su construcción.

La Máquina Analítica

Su trabajo con la máquina diferencial lo llevó a nuevas ideas, y así en 1834 ya tenía realizados los primeros bocetos de la Máquina Analítica, que nunca llegó a construirse pero su diseño sentó las bases de la computadora actual. Pretendía que fuese capaz de realizar cualquier secuencia de instrucciones aritméticas. Para esta realización contó con fondos del gobierno inglés y con la colaboración de la que está considerada como la primera programadora de la historia, Ada Lovelace, hija del poeta Lord Byron. El objetivo de la Máquina Analítica era ser una calculadora de propósito general, controlada por una secuencia de instrucciones, con una unidad de proceso, una memoria central, unidades de entrada y salida de datos (¿les suena conocido?), y la posibilidad de controlar paso a paso las instrucciones, es decir, lo que hoy conocemos como programa.

Esta máquina poseía la mayoría de las características de la computadora moderna. Babbage deseaba que fuera capaz de ejecutar cualquier operación matemática basándose en la alimentación de información por medio de tarjetas perforadas. La máquina de Babbage debería ser capaz de responder con rapidez y exactitud, y proporcionar la solución de los más complejos problemas matemáticos y algebraicos. Además de ese banco de información, la máquina poseía muchas de las características de una moderna computadora: estaba provista de memoria y podía comparar resultados, imprimía las respuestas, procesaba los datos y ¡modificaba su propio programa!

En esencia era una computadora de propósitos generales. La máquina analítica de Babbage podía sumar, restar, multiplicar y dividir en secuencia automática a una velocidad de 60 sumas por minuto, y su diseño requería miles de engranes y mecanismos. Los escépticos le pusieron el sobrenombre de "la locura de Babbage".

Los trazos detallados de Babbage describían las características incorporadas ahora en la moderna computadora electrónica. Si Babbage hubiera vivido en la era de la tecnología electrónica y las partes de precisión, hubiera adelantado el nacimiento de la computadora electrónica en casi un siglo. Irónicamente, su obra se olvidó a tal grado, que algunos pioneros en el desarrollo de la computadora electrónica ignoraron por completo sus conceptos sobre memoria, impresoras, tarjetas perforadas y control de programa secuencial.

Ada Lovelace ayudó a Babbage económicamente y escribió artículos y programas para la referida máquina, algunos de ellos sobre juegos. Sin embargo, este proyecto tampoco pudo realizarse por razones económicas y tecnológicas. Se sabe que Babbage nunca recibió remuneración alguna por sus trabajos, por lo que el Parlamento Inglés decidió ofrecerle un título de nobleza a cambio (le ofrecieron el título de Barón). Babbage rehusó aceptarlo, pidiendo mejor una pensión vitalicia que tampoco llegó a recibir. Sin embargo, ha recibido algo más valioso que cualquier título de nobleza: ser considerado el padre de la computación moderna.

A pesar de que Babbage no pudo construir la máquina analítica, su proyecto supuso sentar las bases de la computación y todos los conceptos por él expuestos en su diseño se demostraron que eran correctos años más tarde. Howard Aiken, director del Proyecto Mark I de la Universidad de Harvard, afirmó: "Si Babbage hubiera vivido 75 años más tarde, yo estaría desempleado".

Babbage, por supuesto, no pudo terminar su invento y, a su muerte, había invertido en él más de 20,000 libras esterlinas. Su genio matemático, demasiado avanzado para su época, intentó algo que sólo más de un siglo después habría de hacerse realidad. En 1830 apareció su libro Reflexiones sobre la Decadencia de la Ciencia en Inglaterra, al que siguieron, en 1832, Una Economía de las Máquinas y las Manufacturas y en 1837, "El noveno Tratado de Bridgewater".

Charles Babbage murió el 24 de octubre de 1871. La Sociedad Real a la que tan fuertemente cuestionara Babbage en vida, no se molestó en imprimirle un obituario, y el Times de Londres lo ridiculizó despiadadamente. Sin duda, fue un triste final para un brillante inventor, matemático, filósofo y sobre todo pensador, poseedor de una aguda mente y una profunda inteligencia.

 

Prefijos Binarios

En el ámbito de la computación se emplean cifras que se expresan casi siempre como potencias de 2, basado en el hecho de que para las computadoras lo normal es lo binario. Inicialmente el prefijo "K" se usaba, y se usa, para expresar el múltiplo más pequeño del byte, unidad de información fundamental, tanto en la memoria principal como en los medios de almacenamiento. La razón es la similitud entre 10^3 y 2^10, que valen, respectivamente, 1000 y 1024. Se escribe en mayúsculas para diferenciarlo de kilo, que es el prefijo que indica el múltiplo 1000 en el Sistema Internacional de Unidades. Posteriormente, a medida que ha crecido la capacidad de almacenamiento de las computadoras, se han ido incorporando nuevos prefijos para expresar múltiplos de byte, tomados directamente del mencionado Sistema Internacional de Unidades, pero basados en potencias de 2. Así lo vemos en la siguiente tabla:

No obstante, el uso incorrecto de los prefijos del Sistema Internacional (con base 10) como si fueran prefijos binarios (con base 2) es causa de serias confusiones. De todas formas, estos prefijos mantienen el significado de las potencias de 10 cuando de lo que se trata es de expresar la velocidad de la transmisión de datos (cantidad de bits): la red Ethernet de 10 Mbps es capaz de transmitir 10.000.000 bps, y no 10.485.760 bps.

El problema se acrecienta por no ser las unidades de información bit y byte unidades del SI. En el SI el bit, el byte, el octeto, el baudio o la cantidad de signos se darían en hertzios. Aunque es más claro emplear "bit" para el bit y "b" para el byte, a menudo se emplea "b" para el bit y "B" para el byte (en el SI, B es la unidad del belio, siendo la del decibelio dB).

El uso convencional sembró confusión: 1024 no es 1000. Los fabricantes de dispositivos de almacenamiento habitualmente usan los factores SI, por lo que un disco duro de 30 GB tiene una capacidad aproximada de 28 * 2^30 bytes, lo que serían 28 GB reales. Los ingenieros en telecomunicaciones también los usan: una conexión de 1 Mbps transfiere 106 bits por segundo. Sin embargo, los fabricantes de disquetes trabajan de otra forma: para ellos, el prefijo M no significa (1000 × 1000) como en el SI, ni (1024 × 1024) como en informática. El disquete común de "1,44 MB" tiene una capacidad de (1,44 × 1000 × 1024) bytes de 8 bits. (Sin olvidar que los disquetes de 3½ pulgadas son en realidad de 90 milímetros.)

En la época de las computadoras de 32K de memoria ROM esta confusión no era muy peligrosa, ya que la diferencia entre 1000 y 1024 es más o menos 2%. En cambio con el acelerado crecimiento de la capacidad de las memorias y de los periféricos de almacenamiento en la actualidad, las diferencias llevan a errores cada vez mayores.

Para tratar de aclarar esta confusión, la Comisión Electrotécnica Internacional (International Electrotechnical Commission IEC) eligió nuevos prefijos binarios en 1998, que consisten en colocar un 'bi' tras la primera sílaba del prefijo decimal (siendo el símbolo binario como el decimal más una 'i'). Por lo tanto, ahora un kilobyte (1 kB) son 1.000 bytes, y un kibibyte (KiB) 2^10 = 1.024 bytes. De la misma forma, mebi (Mi: 2^20), gibi (Gi: 2^30), tebi (Ti: 2^40), pebi (Pi: 2^50) y exbi (Ei: 2^60). Aunque el estándar del IEC nada diga al respecto, los siguientes prefijos alcanzarían hasta zebi (Zi: 2^70) y yobi (Yi: 2^80). Hasta el momento el empleo de estos últimos ha sido muy escaso.

Los nombres IEC están definidos hasta "exbi", correspondiente al prefijo SI "exa". Los otros prefijos, "zetta" (10^21) y "yotta" (10^24) no tienen correspondiente. Por extensión de lo establecido por la norma, se puede sugerir "zebi" (Zi) y "yobi" (Yi) como prefijos para 2^70 y 2^80. Incluso, fuera del ámbito de los organismos de estandarización, se han sugerido los prefijos "bronto" para 2^90 y "geop" para 2^100.

La parte bi del prefijo viene de la palabra binario, por ejemplo, kibibyte significa un kilobinario byte, que es 1024 bytes. Nótese también la K en mayúscula para el símbolo "Kibi-": mientras que la letra para el prefijo análogo en el Sistema Internacional kilo- es una k en minúscula. La K en mayúscula ha sido seleccionada para dar consistencia con otros prefijos y con el uso extendido y erróneo del prefijo del SI (como en "KB").

Para el año 2006 esta convención de nombres ya es empleada por algunos sistemas operativos como GNU/Linux, donde ya existen distribuciones que la exhiben (como Ubuntu), aunque todavía no ha ganado amplia difusión en otros medios.

En la octava edición del Sistema Internacional de Unidades publicada en el año 2006 se especifica que los prefijos del SI se refieren estrictamente a potencias de 10, e indica que los prefijos adoptados por la IEC para potencias binarias en el estándar internacional IEC 60027-2:2005, Símbolos de letras para usarse en tecnología eléctrica - Parte 2: Tele-comunicaciones y electrónica (IEC 60027-2:2005, Letter symbols to be used in electrical technology – Part 2: Telecommunications and electronics) deberían ser usados en el campo de la tecnología de la información para evitar el uso incorrecto de los prefijos del SI, aunque estos prefijos no sean parte del SI.

La IEEE ha aceptado el uso de los prefijos binarios bajo el estándar IEEE 1541 publicado en el año 2002 y elevado a estándar de uso completo en el año 2005. Allí se especifica "B" como el símbolo para el byte (por ejemplo, MB significa megabyte), y "b" como el símbolo para bit; sin embargo la IEC 60027 y el MIXF especifican "bit" (por ejemplo, Mbit para megabit), teniendo la mínima ambigüedad posible de byte "b" vs "B".

Sistema Internacional de Unidades

El Sistema Internacional de Unidades, abreviado SI, es el sistema de unidades más extensamente usado, y que antes se conoció como Sistema Métrico Decimal, que es su antecesor y que se ha mejorado. Fue creado en 1960 por la Conferencia General de Pesas y Medidas, que inicialmente definió seis unidades físicas básicas o fundamentales. En 1971, fue añadida la séptima unidad básica, el mol.

Una de las principales características es que sus unidades están basadas en fenómenos físicos fundamentales. La única excepción es la unidad de la magnitud masa, el kilogramo, que está definida como “la masa del prototipo internacional del kilogramo”, o sea, aquel cilindro de platino e iridio almacenado en una caja fuerte de la Oficina Internacional de Pesos y Medidas.

Las unidades del SI son la referencia internacional de las indicaciones de los instrumentos de medida y a las que están referidas a través de una cadena ininterrumpida de calibraciones o comparaciones. Esto permite alcanzar la equivalencia de las medidas realizadas por instrumentos similares, utilizados y calibrados en lugares apartados y por ende asegurar el cumplimiento de las características de los objetos que circulan en el comercio internacional.

Unidades Básicas

El Sistema Internacional de Unidades consta de siete unidades básicas, también denominadas unidades fundamentales. Son las unidades utilizadas para expresar las magnitudes físicas definidas como fundamentales, a partir de las cuales se definen las demás:

Normas Ortográficas para los Símbolos

• Los símbolos de las unidades no deben tratarse como abreviaturas, por lo que se deben escribir siempre tal cual están definidos. Por ejemplo, m para metro, y A para amperio; por tanto, es incorrecto escribir Kg para kilogramos, mt para metro o seg para segundo.

• Deben usarse preferentemente los símbolos y no los nombres. Por ejemplo, debe escribirse kHz y no kilohertz o kilohertzio.

• Los símbolos no deben pluralizarse, es decir, no debe añadirse una "s" al final. Así, escribirá 10 kilohertz y no 10 kilohertzs, e igualmente 5 kg y no 5 kgs.

• Tampoco debe escribirse un punto (".") al final de un símbolo, salvo cuando el símbolo se encuentra al final de una frase. Por lo tanto, es incorrecto escribir, por ejemplo, el símbolo de kilogramos como "kg." (con el punto). La única manera correcta de escribirlo es "kg". Esto se debe a que se quiere evitar que haya malas interpretaciones; por ejemplo: "Kg", podría entenderse como kelvin•gramo, ya que "K" es el símbolo de la unidad de temperatura kelvin. Por otra parte, ésta última se escribe sin el símbolo de grados "º", pues su nombre correcto no es grado Kelvin (°K), sino sólo kelvin (K).

El SI puede ser usado legalmente en cualquier país del mundo, incluso en aquellos que no lo han implantado. En otros muchos países su uso es obligatorio. En los países que utilizan todavía otros sistemas de unidades de medidas, como los Estados Unidos y el Reino Unido, se acostumbran a indicar las unidades del SI junto a las propias, a efectos de conversión de unidades. El SI fue adoptado por la undécima Conferencia General de Pesos y Medidas (CGPM o Conférence Générale des Poids et Mesures) en 1960.

Prefijos del Sistema Internacional

Los prefijos del SI son prefijos empleados para nombrar a los múltiplos y submúltiplos de cualquier unidad del Sistema Internacional (SI), ya sean unidades básicas o derivadas. Estos prefijos no pertenecen solamente al SI. Muchos de ellos, así como la propia idea de emplearlos, son anteriores al establecimiento del Sistema Internacional en 1960; por lo tanto, se emplean a menudo en unidades que no pertenecen al SI. Los prefijos pertenecientes al SI los fija oficialmente la Oficina Internacional de Pesos y Medidas (Bureau International des Poids et Mesures).

Vistazo General

El prefijo kilo, por ejemplo, multiplica por mil, por lo tanto un kilómetro son 1.000 m, y un kilovatio son 1.000 W. El prefijo mili divide entre mil; por lo tanto, un milímetro es la milésima parte de un metro (se necesitan 1.000 milímetros para completar un metro), y un mililitro es la milésima parte de un litro. Otra de las ventajas del SI es el empleo de un mismo prefijo para cualquier unidad, lo que facilita el aprendizaje y el empleo de dicho sistema. Ejemplos:

5 cm = 5 × 10−2 m = 5 × 0,01 m = 0,05 m
3 MW = 3 × 106 W = 3 × 1.000.000 W = 3.000.000 W

No se pueden poner dos o más prefijos juntos: por ejemplo, 10−9 metros hay que escribirlos como 1 nm, y no 1 mµm. Hay que tener en cuenta antes los prefijos que las potencias; así, "km²" se lee kilómetros cuadrados, no kilo metros-cuadrados. Por ejemplo, 3 km² son 3.000.000 m², no 3.000 m². Es decir, los prefijos del SI en lugar de miles se convierten en multiplicadores de millón en el caso de las potencias de 2, de mil millones en el caso de las potencias de 3 y así sucesivamente.

Son mejores los prefijos cuya potencia es múltiplo de tres. Por ello es preferible emplear "100 m" que "1 hm". Hay, sin embargo, algunas excepciones importantes: el centímetro, la hectárea (hecto-área), el centilitro, el decímetro cúbico (equivalente a un litro), el hectopascal y el decibelio (la décima parte de un belio).

Los prefijos myria- y myrio-, que han quedado obsoletos, se abandonaron antes de que el SI entrara en vigor en 1960, probablemente por no seguir el mismo modelo que el resto de prefijos, por no existir símbolos adecuados para representarlos y por ser, en general, poco empleados.