Operadores Lógicos Binarios – Primera Parte

En el siglo XIX el matemático inglés George Boole formuló todo un cuerpo de teoría donde hace una correspondencia entre los valores veritativos de la Lógica Formal, verdadero y falso, con los números 0 y 1 respectivamente, y la cual se conoce hoy como el Álgebra de Boole. En aquella época quizás muchos se preguntarían para qué podría servir semejante conjunto de definiciones, operaciones y leyes basadas sólo en 2 números. Un siglo después Claude Shannon encontró otra correspondencia, esta vez entre el Álgebra de Boole y los conmutadores electrónicos, introduciendo así el concepto de bit, abriendo de esta manera el camino a la aplicación práctica de esta teoría, que se plasmaría en los denominados circuitos lógicos, base de los sistemas de computación modernos. (1)

Casi todos los lenguajes de programación implementan tipos de datos lógicos o booleanos, y sus respectivos operadores, conocidos generalmente por sus nombres en inglés (and para la conjunción, or para la disyunción inclusiva, xor para la disyunción exclusiva y not para la negación. La implicación está implícita en la sentencia condicional if) (2). Pero también podemos realizar las operaciones lógicas a nivel de los bits de números enteros, a través de los operadores lógicos binarios (bitwise), además de otras como el desplazamiento y la rotación de bits, en lenguajes como C.

Primero veamos los operadores lógicos formales, o sea, aquellos cuyos operandos son expresiones lógicas como las obtenidas mediante los operadores relacionales; recordando además que en el lenguaje C y sus derivados el 0 representa el valor lógico falso y cualquier otro número, generalmente el 1, representa el valor lógico verdadero.

La conjunción se realiza mediante el operador &&, y como hemos visto, el resultado sólo es verdadero si ambos operadores son verdaderos. Ejemplo:

int m = 4, n = 5, p;
p = (m > 0) && (n == 5);
// ambas operaciones relacionales son verdaderas.
// p toma el valor de 1 (verdadero)

if ( (m > n) && (n > 1) ) p = 10;
else p = 20;
// p vale 20, ya que (m > n) es falso y, por tanto, la conjunción
// es falsa

La disyunción inclusiva se lleva a cabo con el operador ||, y es falsa solamente si los dos operandos son falsos. Ejemplo:

int a = 1, b = 2, c = 3;
if ( (a > b) || (c >= a + b) ) c++;
else c = 0;
// como (c >= a + b) es verdadera, la disyunción inclusiva
// es verdadera, y c se incrementa en 1 (c++)

La negación tiene como operador el signo ! e invierte el valor de su único operando lógico. Ejemplo:

int x = 3, y;
if (!x) y = 100;
else y = 10;
// como x es distinto de 0, o sea, verdadero, al negarlo con ! se
// convierte en falso. La variable y vale 10

En cuanto a los operadores lógicos binarios, en C/C++ tenemos los siguientes:

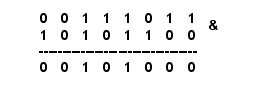
Conjunción Binaria: &.

Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m & n será:

Disyunción Inclusiva Binaria: |

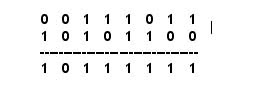
Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m | n será:

Disyunción Exclusiva Binaria: ^:

Sean m = 59 (00111011₂) y n = 172 (10101100₂), entonces m ^ n será:



Negación Binaria (Conocida también como complemento a 1): ~.

Sea m = 59 (00111011₂), entonces ~n será:


Si observamos el valor resultante, comprobamos que se trata del número 196 en decimal, el cual sumado al operando original, o sea el 59, nos da 255, lo que es lo mismo que 2⁸ - 1. En general, el complemento a 1 de un número m de n bits será: ~m = 2ⁿ - m - 1. Si se elimina el -1, hablaríamos del complemento a 2; por lo tanto, el complemento a 2 de un número m es: ~m + 1, que es utilizado para representar números enteros negativos en la computadora.

Las operaciones de desplazamiento de bits permiten justamente eso, mover los bits de un byte, bien sea a la derecha o a la izquierda. Son de mucha utilidad en diversas situaciones, incluso para realizar operaciones aritméticas. Veamos su implementación en el lenguaje C:

Desplazamiento a la Izquierda: <<.

Sea m = 59 (00111011₂), entonces n >> 2 será:

Obsérvese que los bits del número se desplazan 2 espacios a la izquierda, rellenando con 0 los bits menos significativos (los de la derecha). En este caso, si desplazamos más de 2 bits a la izquierda, se perderían bits, lo que se conoce como acarreo. En cuanto al valor resultante, vemos que se trata de 236, o sea, 59 * 4; en general, el desplazamiento a la izquierda de n bits de un número m es igual a: m << n = m * 2ⁿ, siempre y cuando no haya pérdida de bits (acarreo).

Desplazamiento a la Derecha: >>.
Sea n = 172 (10101100₂), entonces n >> 2 será:


Aquí los bits del número se desplazan 2 espacios a la derecha, rellenando con 0 los bits más significativos (los de la izquierda). Igualmente, si desplazamos más de 2 bits se perderían bits. El resultado es 43, es decir, 172 / 4; en general, el desplazamiento a la derecha de n bits de un número m es igual a: m >> n = m / 2ⁿ, siempre y cuando no haya pérdida de bits (acarreo).