Presentamos ahora algunas aplicaciones utilizando los operadores lógicos binarios, implementando una biblioteca de funciones de utilidad general, y un pequeño programa demostrativo de dichas funciones, las cuales pasamos a describir brevemente, aclarando que los números manejados son del tipo unsigned char, es decir, números enteros positivos de un byte. printbits: Recibe un número en decimal y lo escribe en binario. Utiliza la función condicional implícita. onoff: Recibe un número en decimal y la posición de un bit, y determina si ese bit está encendido (1) o apagado (0). put_on: Recibe un número en decimal y la posición de un bit y lo enciende, es decir, lo convierte en 1. put_off: Recibe un número en decimal y la posición de un bit y lo apaga, es decir, lo convierte en 0. right_rot : Recibe un número en decimal (x) y un número entre 0 y 7 (n), y rota n posiciones a la derecha los bits de x. left_rot : Recibe un número en decimal (x) y un número entre 0 y 7 (n), y rota n posiciones a la izquierda los bits de x. change_nibbles: Recibe un número en decimal e Intercambia sus nibbles. right_nibble: Recibe un número en decimal y devuelve su nibble derecho left_nibble: Recibe un número en decimal y devuelve su nibble izquierdo #include <stdio.h> // Escribe un numero en binario
// Biblioteca de funciones de manipulacion de bits
// bits.h
void printbits(unsigned char x) {
for (int i = 7; i >= 0; i--)
printf("%c", (x & (1 << i)) ? '1' : '0');
}
// Determina si el bit n de un byte esta encendido (1) o apagado (0)
unsigned char onoff(unsigned char x, unsigned char n) {
if (x & (1 << n)) return 1;
else return 0;
}
// Enciende un bit
unsigned char put_on(unsigned char x, unsigned char n) {
return x |(1 << n);
}
// Apaga un bit
unsigned char put_off(unsigned char x, unsigned char n) {
return x & (255 - (1 << n));
}
// Realiza la rotacion a la derecha
unsigned char right_rot(unsigned char x, unsigned char n) {
return (x >> n) | (x << (8 - n));
}
// Realiza la rotacion a la izquierda
unsigned char left_rot(unsigned char x, unsigned char n) {
return (x << n) | (x >> (8 - n));
}
// Intercambia los nibbles (4 bits) de un byte
unsigned char change_nibbles(unsigned char x) {
return (x << 4) | (x >> 4);
}
// Obtiene el nibble izquierdo
unsigned char left_nibble(unsigned char x) {
return x >> 4;
}
// Obtiene el nibble derecho
unsigned char right_nibble(unsigned char x) {
return x & 15;
}
Listado 1. bits.h
Y ahora el programa ejemplo para demostrar el uso de las funciones de la biblioteca.
// Manejo de bits
// bits.cpp
#include <stdio.h>
#include <conio.h>
#include <C:\BC5\Programas\bits.h> // Ubicar la ruta del archive de biblioteca
unsigned char m1, m2, n1, n2, x, y, z;
void NuevaLinea();
void main() {
m1 = m2 = 59;
n1 = n2 = 172;
printf("Valores originales.\n");
printf(" 76543210\n");
printf("m1 = %3d = ", m1); printbits(m1); NuevaLinea();
printf("n1 = %3d = ", n1); printbits(n1); NuevaLinea();
printf("El bit 4 de m1 vale %d\n", onoff(m1, 5) ? 1 : 0);
printf("El bit 4 de n1 vale %d\n", onoff(n1, 4) ? 1 : 0);
NuevaLinea();
printf("Se enciende el bit 6 de %3d. Resultado en x.\n", m2);
x = put_on(m2, 6);
printf(" 76543210\n");
printf(" x = %3d = ", x); printbits(x); NuevaLinea();
printf("El bit 6 de x vale %d\n", onoff(x, 4) ? 1 : 0);
NuevaLinea();
printf("Se apaga el bit 5 de %3d. Resultado en y.\n", n2);
y = put_off(n2, 5);
printf(" 76543210\n");
printf(" y = %3d = ", y); printbits(y); NuevaLinea();
printf("El bit 5 de y vale %d\n", onoff(y, 5));
NuevaLinea();
m2 = m1; n2 = n1;
printf("%3d se rota 3 bits a la derecha. Resultado en x.\n", m2);
x = right_rot(m2, 3);
printf(" 76543210\n");
printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
printf(" x = %3d = ", x); printbits(x); NuevaLinea();
NuevaLinea();
printf("%3d se rota 3 bits a la izquierda. Resultado en y.\n", n2);
y = left_rot(n2, 3);
printf(" 76543210\n");
printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
printf(" y = %3d = ", y); printbits(y); NuevaLinea();
NuevaLinea();
m2 = m1; n2 = n1;
printf("Se intercambian los nibbles de %3d. Resultado en x.\n", m2);
x = change_nibbles(m2);
printf(" 76543210\n");
printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
printf(" x = %3d = ", x); printbits(x); NuevaLinea();
NuevaLinea();
printf("Se intercambian los nibbles de %3d. Resultado en y.\n", n2);
y = change_nibbles(n2);
printf(" 76543210\n");
printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
printf(" y = %3d = ", y); printbits(y); NuevaLinea();
NuevaLinea();
m2 = m1; n2 = n1;
printf("Se obtiene el nibble izquierdo de %3d. Resultado en x.\n", m2);
x = left_nibble(m2);
printf(" 76543210\n");
printf("m2 = %3d = ", m2); printbits(m2); NuevaLinea();
printf(" x = %3d = ", x); printbits(x); NuevaLinea();
NuevaLinea();
printf("Se obtiene el nibble derecho de %3d. Resultado en y.\n", n2);
y = right_nibble(n2);
printf(" 76543210\n");
printf("n2 = %3d = ", n2); printbits(n2); NuevaLinea();
printf(" y = %3d = ", y); printbits(y); NuevaLinea();
NuevaLinea();
getch();
}
void NuevaLinea() {
printf("\n");
}
Listado 2. bits.cpp
martes, 5 de febrero de 2008
Operadores Lógicos Binarios – Segunda Parte
Publicado por neriovf en 23:05 0 comentarios
Etiquetas: Lógica, Programación
Operadores Lógicos Binarios – Primera Parte
En el siglo XIX el matemático inglés George Boole formuló todo un cuerpo de teoría donde hace una correspondencia entre los valores veritativos de la Lógica Formal, verdadero y falso, con los números 0 y 1 respectivamente, y la cual se conoce hoy como el Álgebra de Boole. En aquella época quizás muchos se preguntarían para qué podría servir semejante conjunto de definiciones, operaciones y leyes basadas sólo en 2 números. Un siglo después Claude Shannon encontró otra correspondencia, esta vez entre el Álgebra de Boole y los conmutadores electrónicos, introduciendo así el concepto de bit, abriendo de esta manera el camino a la aplicación práctica de esta teoría, que se plasmaría en los denominados circuitos lógicos, base de los sistemas de computación modernos. (1) Casi todos los lenguajes de programación implementan tipos de datos lógicos o booleanos, y sus respectivos operadores, conocidos generalmente por sus nombres en inglés (and para la conjunción, or para la disyunción inclusiva, xor para la disyunción exclusiva y not para la negación. La implicación está implícita en la sentencia condicional if) (2). Pero también podemos realizar las operaciones lógicas a nivel de los bits de números enteros, a través de los operadores lógicos binarios (bitwise), además de otras como el desplazamiento y la rotación de bits, en lenguajes como C. Primero veamos los operadores lógicos formales, o sea, aquellos cuyos operandos son expresiones lógicas como las obtenidas mediante los operadores relacionales; recordando además que en el lenguaje C y sus derivados el 0 representa el valor lógico falso y cualquier otro número, generalmente el 1, representa el valor lógico verdadero. int m = 4, n = 5, p; if ( (m > n) && (n > 1) ) p = 10; La disyunción inclusiva se lleva a cabo con el operador ||, y es falsa solamente si los dos operandos son falsos. Ejemplo:
La conjunción se realiza mediante el operador &&, y como hemos visto, el resultado sólo es verdadero si ambos operadores son verdaderos. Ejemplo:
p = (m > 0) && (n == 5);
// ambas operaciones relacionales son verdaderas.
// p toma el valor de 1 (verdadero)
else p = 20;
// p vale 20, ya que (m > n) es falso y, por tanto, la conjunción
// es falsa
int a = 1, b = 2, c = 3;
if ( (a > b) || (c >= a + b) ) c++;
else c = 0;
// como (c >= a + b) es verdadera, la disyunción inclusiva
// es verdadera, y c se incrementa en 1 (c++)
La negación tiene como operador el signo ! e invierte el valor de su único operando lógico. Ejemplo:
int x = 3, y;
if (!x) y = 100;
else y = 10;
// como x es distinto de 0, o sea, verdadero, al negarlo con ! se
// convierte en falso. La variable y vale 10
En cuanto a los operadores lógicos binarios, en C/C++ tenemos los siguientes:
Conjunción Binaria: &.
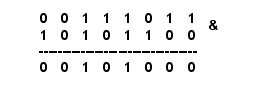
Sean m = 59 (001110112) y n = 172 (101011002), entonces m | n será:
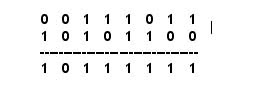
Disyunción Exclusiva Binaria: ^:
Sean m = 59 (001110112) y n = 172 (101011002), entonces m ^ n será:
Negación Binaria (Conocida también como complemento a 1): ~.
Sea m = 59 (001110112), entonces ~n será:
Si observamos el valor resultante, comprobamos que se trata del número 196 en decimal, el cual sumado al operando original, o sea el 59, nos da 255, lo que es lo mismo que 28 - 1. En general, el complemento a 1 de un número m de n bits será: ~m = 2n - m - 1. Si se elimina el -1, hablaríamos del complemento a 2; por lo tanto, el complemento a 2 de un número m es: ~m + 1, que es utilizado para representar números enteros negativos en la computadora.
Las operaciones de desplazamiento de bits permiten justamente eso, mover los bits de un byte, bien sea a la derecha o a la izquierda. Son de mucha utilidad en diversas situaciones, incluso para realizar operaciones aritméticas. Veamos su implementación en el lenguaje C:
Desplazamiento a la Izquierda: <<.
Sea m = 59 (001110112), entonces n >> 2 será:

Obsérvese que los bits del número se desplazan 2 espacios a la izquierda, rellenando con 0 los bits menos significativos (los de la derecha). En este caso, si desplazamos más de 2 bits a la izquierda, se perderían bits, lo que se conoce como acarreo. En cuanto al valor resultante, vemos que se trata de 236, o sea, 59 * 4; en general, el desplazamiento a la izquierda de n bits de un número m es igual a: m << n = m * 2n, siempre y cuando no haya pérdida de bits (acarreo).
Desplazamiento a la Derecha: >>.
Sea n = 172 (101011002), entonces n >> 2 será:
Aquí los bits del número se desplazan 2 espacios a la derecha, rellenando con 0 los bits más significativos (los de la izquierda). Igualmente, si desplazamos más de 2 bits se perderían bits. El resultado es 43, es decir, 172 / 4; en general, el desplazamiento a la derecha de n bits de un número m es igual a: m >> n = m / 2n, siempre y cuando no haya pérdida de bits (acarreo).
Publicado por neriovf en 0:55 0 comentarios
Etiquetas: Lógica, Programación
domingo, 3 de febrero de 2008
Proposición Lógica
La proposición es la expresión lingüística del razonamiento, que se caracteriza por ser verdadera o falsa empíricamente, sin ambigüedades. Son proposiciones las oraciones aseverativas, las leyes científicas, las fórmulas matemáticas, las fórmulas y/o esquemas lógicos, los enunciados cerrados o claramente definidos. No son proposiciones las opiniones y suposiciones; los proverbios, modismos y refranes; los enunciados abiertos no definidos; las oraciones interrogativas, exclamativas, imperativas, desiderativas y dubitativas; las interjecciones en general; ni las operaciones aritméticas.
El valor de verdad de una proposición depende no solamente de las relaciones entre las palabras del lenguaje y los objetos en el mundo, sino también del estado del mundo y del conocimiento acerca de ese estado. El valor de verdad de la oración Juan canta depende no solamente de la persona denotada en Juan y el significado del verbo cantar, sino también del momento cuando esta oración es expresada. Juan probablemente canta ahora, pero ciertamente que no siempre está cantando.
De la misma manera, debemos hacer una distinción entre la oración gramatical propiamente dicha, a la que llamaremos enunciado, y el contenido o significado del enunciado, que es la proposición. Así los siguientes enunciados representan en realidad a la misma proposición:
- En Maracaibo hace mucho calor
- Maracaibo es una ciudad muy calurosa
- La temperatura media de Maracaibo es bastante alta
- El clima de Maracaibo es cálido
- Maracaibo is a hot city
Las siguientes expresiones son ejemplos de proposiciones:
- Bolívar libertó a Venezuela
- El hierro es un mineral
- Einstein fue un físico teórico
- 36 + 63 = 99
- La palabra "esdrújula" es esdrújula
Los siguientes son ejemplos de expresiones las cuales no son proposiciones
- El hombre más fuerte del mundo
- El director del periódico
- ¡Quién se ganara el Kino!
- 13 + 7
- ¡Tú te callas!
- X obtuvo el Premio Nobel en 1970
- ¿Cuánto cuesta ese reloj?
Las proposiciones se representan por letras minúsculas: p, q, r, s, t, u, etc. Por ejemplo, sea la proposición q igual a 34 + 56 = 90
CLASIFICACION
Proposiciones Simples o Atómicas
Son aquellas que carecen totalmente de conectivos lógicos y que, por lo tanto, son inseparables. En este grupo se encuentran las proposiciones predicativas, que son aquellas en la cual se afirma o atribuye una característica respecto de un objeto, como por ejemplo, Juan Pérez es profesor; y las proposiciones relacionales, en las cuales existe una relación de dependencia, estableciendo un enlace entre dos o más objetos, como por ejemplo, Caracas es la capital de Venezuela.
Proposición Compuesta o Molecular
Son aquellas que resultan de la combinación de varias proposiciones simples, unidas por uno o más conectivos lógicos y que pueden ser separadas y descompuestas en proposiciones más simples. Su valor de verdad depende del de las proposiciones que la componen.
CONECTIVOS LÓGICOS
NEGACION

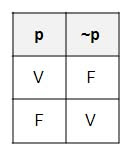
Tabla de Verdad de la Negación
CONJUNCIÓN

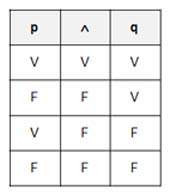

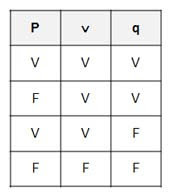





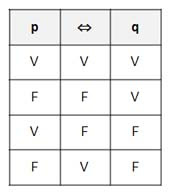
Tabla de Verdad de la Equivalencia
Publicado por neriovf en 15:19 9 comentarios
Etiquetas: Lógica





