Casi todos los lenguajes de programación implementan tipos de datos lógicos o booleanos, y sus respectivos operadores, conocidos generalmente por sus nombres en inglés (and para la conjunción, or para la disyunción inclusiva, xor para la disyunción exclusiva y not para la negación. La implicación está implícita en la sentencia condicional if) (2). Pero también podemos realizar las operaciones lógicas a nivel de los bits de números enteros, a través de los operadores lógicos binarios (bitwise), además de otras como el desplazamiento y la rotación de bits, en lenguajes como C.
Primero veamos los operadores lógicos formales, o sea, aquellos cuyos operandos son expresiones lógicas como las obtenidas mediante los operadores relacionales; recordando además que en el lenguaje C y sus derivados el 0 representa el valor lógico falso y cualquier otro número, generalmente el 1, representa el valor lógico verdadero.
La conjunción se realiza mediante el operador &&, y como hemos visto, el resultado sólo es verdadero si ambos operadores son verdaderos. Ejemplo:
int m = 4, n = 5, p;
p = (m > 0) && (n == 5);
// ambas operaciones relacionales son verdaderas.
// p toma el valor de 1 (verdadero)
if ( (m > n) && (n > 1) ) p = 10;
else p = 20;
// p vale 20, ya que (m > n) es falso y, por tanto, la conjunción
// es falsa
La disyunción inclusiva se lleva a cabo con el operador ||, y es falsa solamente si los dos operandos son falsos. Ejemplo:
int a = 1, b = 2, c = 3;
if ( (a > b) || (c >= a + b) ) c++;
else c = 0;
// como (c >= a + b) es verdadera, la disyunción inclusiva
// es verdadera, y c se incrementa en 1 (c++)
La negación tiene como operador el signo ! e invierte el valor de su único operando lógico. Ejemplo:
int x = 3, y;
if (!x) y = 100;
else y = 10;
// como x es distinto de 0, o sea, verdadero, al negarlo con ! se
// convierte en falso. La variable y vale 10
En cuanto a los operadores lógicos binarios, en C/C++ tenemos los siguientes:
Conjunción Binaria: &.

Sean m = 59 (001110112) y n = 172 (101011002), entonces m | n será:
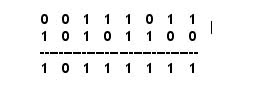
Disyunción Exclusiva Binaria: ^:
Sean m = 59 (001110112) y n = 172 (101011002), entonces m ^ n será:
Negación Binaria (Conocida también como complemento a 1): ~.
Sea m = 59 (001110112), entonces ~n será:
Si observamos el valor resultante, comprobamos que se trata del número 196 en decimal, el cual sumado al operando original, o sea el 59, nos da 255, lo que es lo mismo que 28 - 1. En general, el complemento a 1 de un número m de n bits será: ~m = 2n - m - 1. Si se elimina el -1, hablaríamos del complemento a 2; por lo tanto, el complemento a 2 de un número m es: ~m + 1, que es utilizado para representar números enteros negativos en la computadora.
Las operaciones de desplazamiento de bits permiten justamente eso, mover los bits de un byte, bien sea a la derecha o a la izquierda. Son de mucha utilidad en diversas situaciones, incluso para realizar operaciones aritméticas. Veamos su implementación en el lenguaje C:
Desplazamiento a la Izquierda: <<.
Sea m = 59 (001110112), entonces n >> 2 será:

Obsérvese que los bits del número se desplazan 2 espacios a la izquierda, rellenando con 0 los bits menos significativos (los de la derecha). En este caso, si desplazamos más de 2 bits a la izquierda, se perderían bits, lo que se conoce como acarreo. En cuanto al valor resultante, vemos que se trata de 236, o sea, 59 * 4; en general, el desplazamiento a la izquierda de n bits de un número m es igual a: m << n = m * 2n, siempre y cuando no haya pérdida de bits (acarreo).
Desplazamiento a la Derecha: >>.
Sea n = 172 (101011002), entonces n >> 2 será:
Aquí los bits del número se desplazan 2 espacios a la derecha, rellenando con 0 los bits más significativos (los de la izquierda). Igualmente, si desplazamos más de 2 bits se perderían bits. El resultado es 43, es decir, 172 / 4; en general, el desplazamiento a la derecha de n bits de un número m es igual a: m >> n = m / 2n, siempre y cuando no haya pérdida de bits (acarreo).

No hay comentarios:
Publicar un comentario